球体 锥体与柱体 圆与圆周率 Mathigon 球の体積の公式から、表面積Sは、 (4/3) π r 3 = (1/3)・S・r より、S = 4 π r 2 以上から、 (球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r(円の面積) = π r 2 という公式が作られる。 円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。
1
球体面積 公式
球体面積 公式-V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin表面積 s S p h e r e ( 1 ) v o l u m e V = 4 3 π r 3 ( 2 ) s u r f a c e a r e a S = 4 π r 2 S p h e r e ( 1 ) v o l u m e V = 4 3 π r 3 ( 2 ) s u r f a c e a r e a S = 4 π r 2



圆球表面积 球体表面积的公式证明 篆体字转换器
球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、 4 ×円と球の公式 \(D\):直径 \(\rho\):密度 円の面積 \(\left ( \displaystyle \frac {\pi}{4} \right ) D^2\) 円周 perimeter \(\pi D\) 円形度 circularity (等面積円の円周)/(周長) 球の表面積数学 、算数で、球について 下記2つの公式が成り立つ理由を教えてください。 球体の表面積は、球の半径をr、面積をSとすると、「S=4πr2」 球体積の公式は「V=4─3πr3」回転体の表面積も求めよう
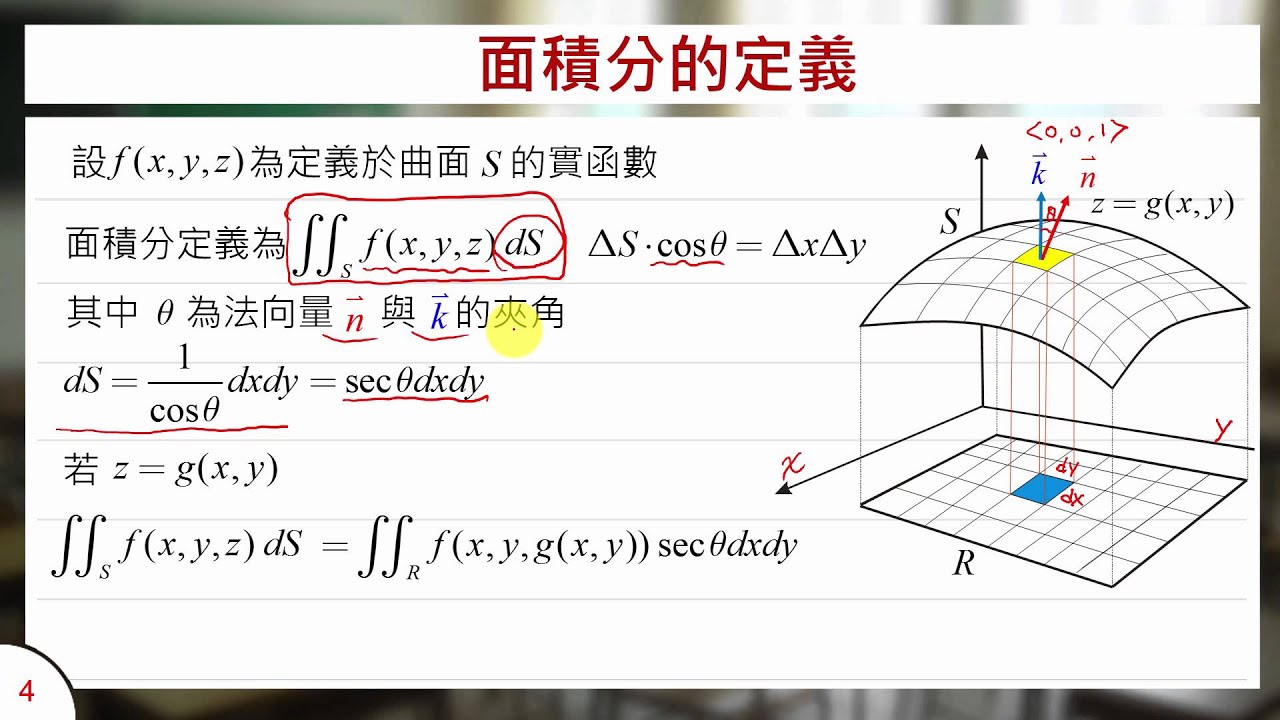
まずは、球の表面積の公式を使います。球の表面積の公式は4πr 2 でしたね。 よって、 4π×3 2 =36π です。しかし、今回は半球なので、36πの半分となり、 18π・・・① となります。 まだこれで終わりではありません! 半球の底の部分を足していませんね!球体 面積 体積 公式ぐー477 ④ 球の体積 半径が7の球の体積をしとすると, リーまァが ー 考え方と解き方 面積と体積を求める公式にあてはめて 面積 4ァ x6=144z(cmう) *積 芋zx6'=2z(om 3 國 表面積 144zcm 体積 2rem 球の表面積はその球がちょ うと人 る円柱の側面積曲面積の公式の仕組みを少しだけですが解説します。 曲面積を求めるにあたって、\( x \), \( y \) をそれぞれ \( \Delta x \), \( \Delta y \) だけ 微小変化させることで作った微小な面積の平行四辺形 を考えます。 曲面 \( z = f(x,y) \) で与えられた面を微小な平行四辺形に分割し、分割した平行四
優雅 球体 表面積 求め 方 球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説し 中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学び 球の表面積と体積の公式 数学fun 中学数学 球の体積の求め方の公式を1発で覚える方法半径 ってわけだね。 たとえば、半径30cm のサッカーボールがあったとしよう。 このボールの皮の面積、つまり表面積は、楕円体の体積 体積 V = 4π a b c /3 楕円体の表面積 (楕円面の表面積) a ≧ b ≧ c ならば、表面積は楕円積分を用いて次式で与えられる。




直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com



1
球の体積と表面積の公式: 半径 r r r の球の表面積は S = 4 π r 2 , S=4\pi r^2,\ S = 4 π r 2 , 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。冒頭に述べた球面三角形の面積公式 s = r 2 (a b c − π) s=r^2(abc\pi) s = r 2 (a b c − π) を証明します。 まず二つの大円のなす角が A A A である状況を考えます。球体表面积是指 球面 所围成的几何体的 面积 ,它包括球面和球面所围成的空间,球体表面积的计算公式为S=4πr²=πD²,该公式可以利用球体积求导来计算。 中文名 球体表面积 外文名 Sphere surface area 形 状 球体 公 式 S=4πr²=πD²



面積分 Youtube




すごい球体面積公式 壁紙配布
球体 面積 公式 球体 面積 公式球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 1 2 ⋅4πR2 = 2πR2 1 2 ⋅ 4 π R 2 = 2 π R 2球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。




椭球体表面积公式 椭球表面积怎么算 三人行教育网 Www 3rxing Org



在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻
円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1 2πr ×複雑な公式であっても、その場で思い出すことができますね! 私は今でも語呂合わせで思い出すことがありますw あ! 語呂合わせで公式は覚えたけど どっちが体積で、どっちが表面積だっけ? というようにごちゃごちゃになっちゃう人も多いです。球体 の 表面積 の 求め 方 球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球体面积公式推导图解 搜狗图片搜索



球体面积公式推导图解 搜狗图片搜索
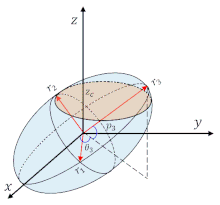
楕円の面積の公式 \(\pi ab\) もちろん(1A)の方法で計算することもできますが、面倒なので(1C)の方法を駆使して楕円の面積を求めたいと思います。 まず、楕円体のまま体積を計算するのはめんどうなので、楕円体を球体に変換してやりましょう。球の体積を求める公式は、V = 4/3 πr^3 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。これが求める半径1の4次元球体の体積です。 5 「4次元の球」の「表面積」 「4次元の球」の「表面積」の公式を求めてみましょう。 まず、半径がrの「4次元の球」の「4次元的な体積」の公式を出します。「4次元的な 体積」はr4 に比例します。ですから、公式は



各图形面积体积公式 搜狗图片搜索




椭球 维基百科 自由的百科全书
球の質量基準比表面積(単位質量当たりの表面積) \\(\\displaystyle \\frac {6}{D \\rho}\\) いちいち半径の公式から換算するのは能率が悪い。 円と球の公式表面積は3通りの方法を解説します。 積分の感覚をつかむよい練習になります。 球の体積と表面積の公式によって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる



球的体积公式和表面积公式 高三网



多变量微积分笔记 球坐标系 我是8位的 博客园
/ 数学公式集 / 体積 漠然と、立方体の辺の長さが2倍になれば大きさが4倍になるのと同じように、球体も直径が2倍になれば表面積も4倍になるかなと思っていたが、実際に計算してみて、間違っていなかったのは少し感動した。球体表面積公式(球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。π = π2 4 πr2



球体积的前世今生 科普中国



官方双语 为什么球的表面积是同样半径圆的面积的四倍 哔哩哔哩 つロ干杯 Bilibili
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。このページでは、円や球という図形に的を絞って、その面積や体積・表面積の公式を、直 感的に求める方法について整理しておきたい。 出発点は、まず円周率である。 球体 锥体与柱体 圆与圆周率 Mathigon 球体 面積 体積 公式球の表面積比と体積比 ここでは球の表面積比と体積比について説明します。 ちなみに、基本的に球はすべて相似な図形です。 半径がrの球と、半径がkrの2つの球があったとします。このときの球の表面積比と体積比について考えてみましょう。 表面積比 半径が



球体积怎么求公式 百度经验



椭圆球表面积公式球体表面积公式
球の表面積の公式、S=4πr 2 とは違ってしまう。 これは、円周の長さを x 方向に積分 するときに、xを微小増加させたときの表面積の変化量が x=0 付近と x=r 付近で異なり、x=r 付近の方が表面積の増加量が大きいためと考えられる。




球的表面积公式 球的表面积公式画法




球体表面积及体积的推导 每日头条




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球体体积 球体面积计算公式 百度经验



椭球 维基百科 自由的百科全书
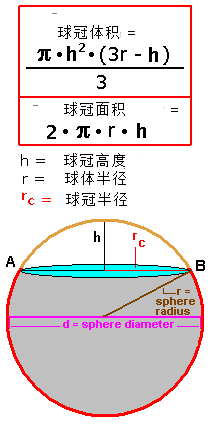



球冠在线计算器 在线计算 在线计算器 计算器在线计算



球的表面積的求法 中學數學課 隨意窩xuite日誌




圆球表面积公式用微积分如何推导 知乎




用感覺理解球體表面積公式 Youtube



球体面积公式推导图解 搜狗图片搜索



球体体积公式推导图解 万图壁纸网




数学趣谈 球面积公式的不同导出方法 参考网




求球体的表面积和体积 修也 Csdn博客



Q Tbn And9gcqzkudsal3galmxwro65pdnhz6flxjjkxas5i6eaqlha2sgymk7 Usqp Cau




3种方法来计算球体的半径




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫
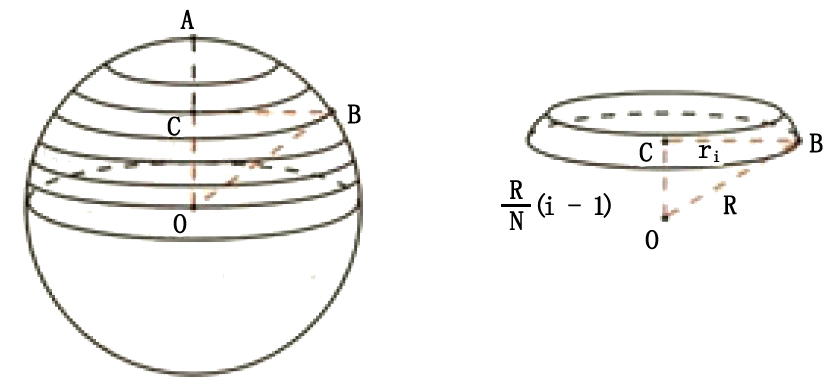



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客



不完整球体表面积求不规则半球体的表面积




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org




高中立體幾何 巧求空間幾何體的體積的三個方法 雪花新闻



球体表面积公式球体表面积球体表面积 公式证明 爱华网




橢球 一種二次曲面 是橢圓在三維空間的推廣 橢球在xyz 笛卡兒坐標系中的方程是 X 華人百科



球体体积公式 怎样计算球体的体积



梯形体积公式梯形体积公式 一加一



Led屏各种面积 计算办法汇总点击查看 临沂led Led显示屏 临沂全彩显示屏 枣庄led 泰安led 日照led大屏幕 航空箱 航空箱厂家 航空箱生产厂家 山东鹰视电子科技有限公司



物理方法解决数学问题 二 Archimedes与球体积公式 Matrix67 The Aha Moments
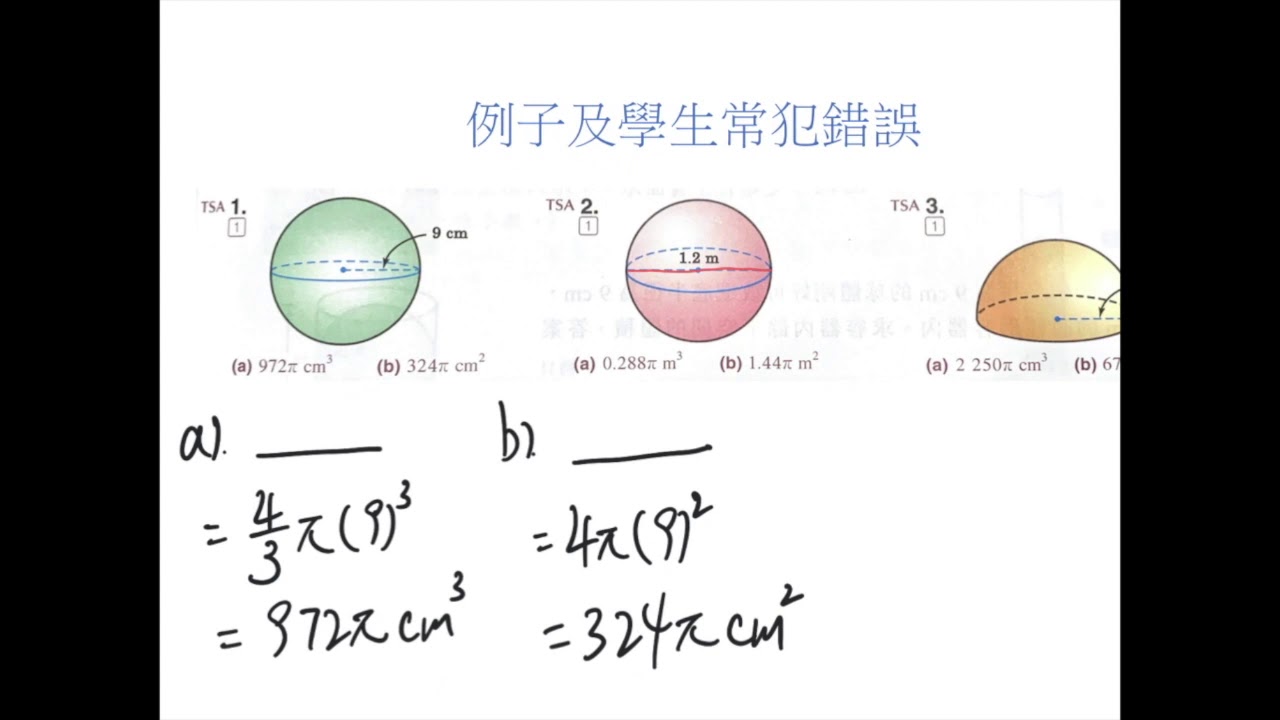



球體體積 總表面面積 Youtube




球的体积的公式推导 如何用微积分知识推导球的体积公式 三人行教育网 Www 3rxing Org




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科




旋轉體的側表面積040 正修科技大學微積分課程6 5 Youtube




球の表面積と体積の公式 数学fun



球体面积公式推导图解 搜狗图片搜索




球冠面积 Stereohomology Csdn博客 球冠面积




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com
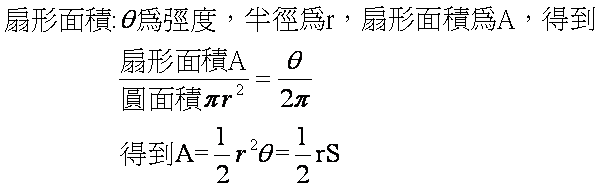



扇形的弧長與面積



在球的体积公式中 为什么会出现三分之四这个奇怪的



球的體積



用微积分解答半径为a的球的表面积 作业 慧海网



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社 自媒体学习平台



所有体积公式大全数学面积体积公式 朵拉利品网



写给5年级的学生 球公式是如何推导出来的 表面积




微分でつなげる円や球の公式 すうがくブログ 式変形ch




斜棱柱体体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com
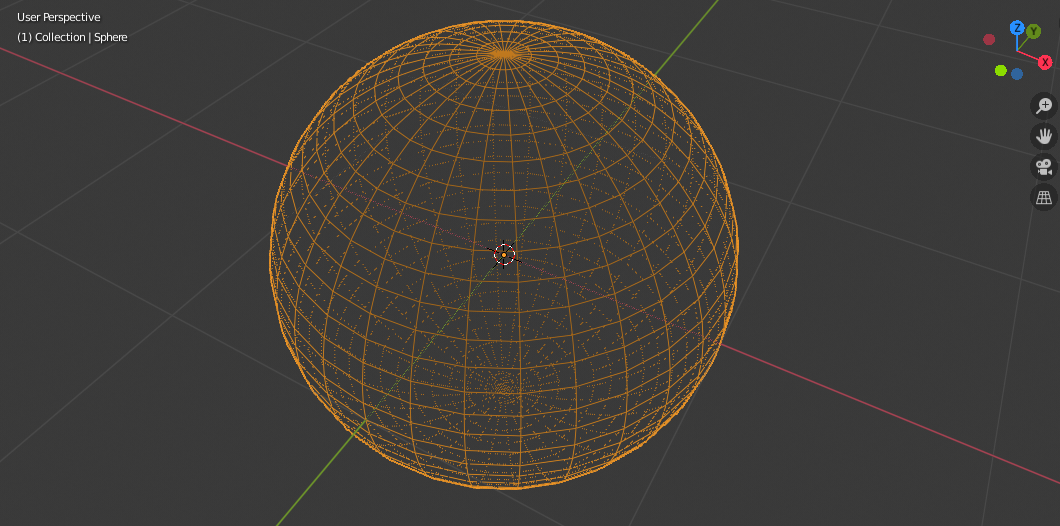



漫谈超球体的体积公式 知乎



球體的體積及表面面積 哔哩哔哩 Bilibili
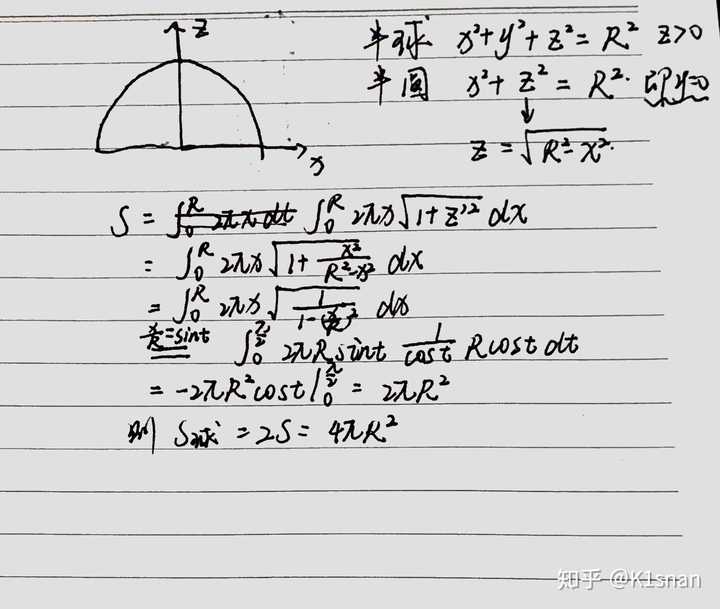



为何对圆周长公式积分无法得到球表面积公式 知乎




7 3b球體的表面面積 Youtube




球の表面積と体積の公式 数学fun
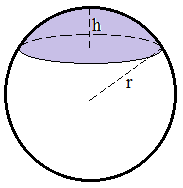



球冠体积 表面积在线计算器



圆球表面积 球体表面积的公式证明 篆体字转换器



球体面积公式推导图解 搜狗图片搜索
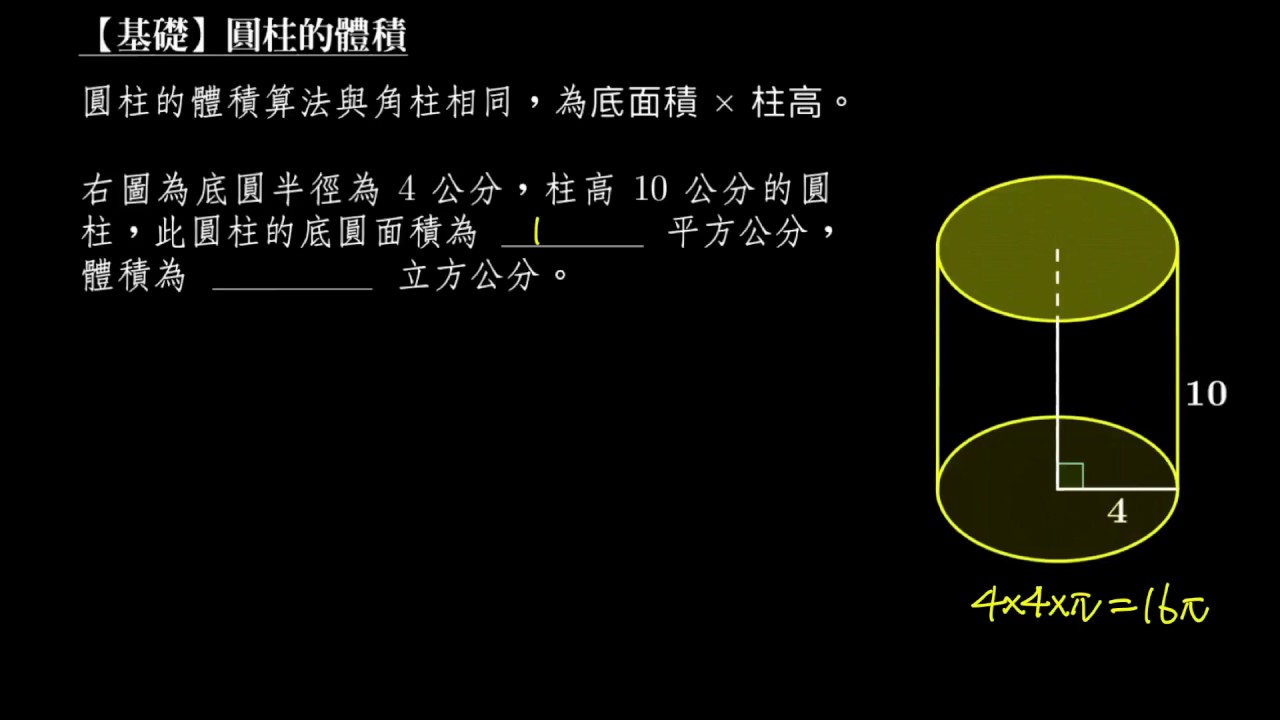



基礎 圓柱的體積 Youtube
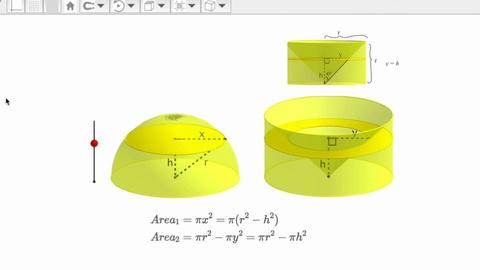



如何使用高中知识推导球体表面积 知乎



悟空问答 为什么球的体积是4 3pr 3 这里为什么是4 3 有什么特别的地方吗 19个回答



球冠体积公式推导 请问在不知道球半径的情况下 怎么计算球冠的面积和体积 图片上这种面积怎么算 三人行教育网 Www 3rxing Org




球の表面積と体積の公式 数学fun




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




椭球中椭圆的面积公式 椭球截面面积公式是什么 我知道是椭圆 我知道椭圆公式 我想知道那个与z轴还有关系的那个公式 三人行教育网 Www 3rxing Org



1




球體表面積及體積的推導 每日頭條



扇形的体积公式 土嘎嘎




012 球的体积空间几何体高中数学 Youtube



球体面积公式推导图解 搜狗图片搜索




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com




球的表面积公式是什么 球体积 表面积公式是



写给5年级的学生 球公式是如何推导出来的 表面积




用感覺理解球體表面積公式 Youtube
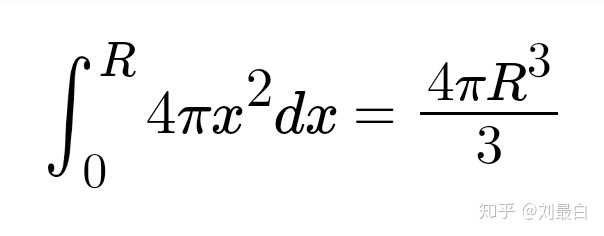



为什么计算圆的周长与面积 球的表面积与体积 使用的都是p 而不是三个不同的数 是偶然还是必然 知乎



微积分下的不规则图形的体积计算原理 科学探索



写给5年级的学生 球公式是如何推导出来的 表面积



球的体积公式 球的体积公式画法
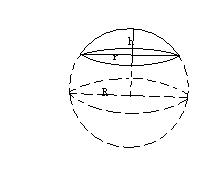



球冠 维基百科 自由的百科全书



球体面积公式推导图解 搜狗图片搜索




球缺体积和球冠表面积的计算公式及应用 晨起尘又落 Csdn博客 球缺的体积公式



球面积 手机壁纸 电脑壁纸 桌面壁纸 图客网
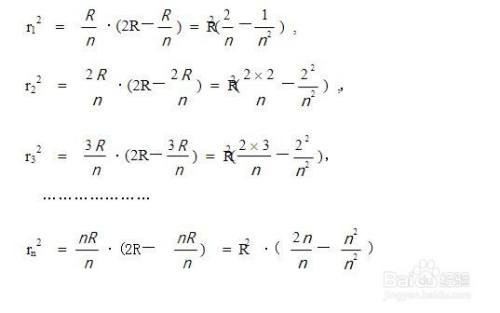



球体体积公式推导图解 百度经验




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



Q Tbn And9gcq8yqurcjtpm Fqjmjdphieds3lspifphn4v0 Ikke4jaabliue Usqp Cau




圆锥与球与圆柱




数学趣谈 球面积公式的不同导出方法 参考网



球体体积公式是球体体积公式是什么




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网




用感覺理解球體表面積公式 Youtube




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科



数学一分钟球的体积公式推导证明 哔哩哔哩 つロ干杯 Bilibili



球体面积公式推导图解 搜狗图片搜索



球的表面积公式推导 万图壁纸网




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com


